引入

我们需要实现这样一个需求: 假设你患有赛博收集癖症状, 每天都高强度从pixiv和各种涩图群收集大量二刺螈cg到自己的硬盘里, 很快你的硬盘里就收集到了数万张来源、清晰度等各不相同的cg.

然而你发现你下载的cg中有相当一部分是重复的, 这些重复的cg占用了你宝贵的磁盘空间, 而你使用的还是一个无法扩容的 Microsoft Surface Pro 64G版, 去除掉系统占用、保留空间等等只剩下十多G的空间了. 因此你急切需要一个快速找出你的cg目录下重复图片并去重的方法. 由于下载来源各不相同, 因此使用文件名等等传统的查找方式显然就无法解决这个问题，必须要从分析图片内容入手.

今天介绍的图像哈希与vp树, 就可以解决这样的问题.

为什么使用图像哈希

通常，我们在校验和比较不同的文件时，一般会对文件使用一种散列哈希算法(aka Cryptographic hash, 例如SHA1, SHA256, 或者在对安全性要求不高的场景使用CRC32等)来提取文件的"特征"。相比巨大的文件本身，文件哈希值更加容易被检索、索引。但是密码学散列哈希有一个特点，即使输入的内容只相差1bit，都会导致哈希结果完全改变，并且这种变化是不可预测的。

而在查找重复图像的过程中，图片可能会经过编码格式转换、颜色空间转换、调色、压缩、变更分辨率等等不会影响图片特征，但是会导致处理前后文件内容相差很大的操作。我们希望有一个哈希算法可以容忍这些由编码与压缩等带来的差异，并且可以评价不同图片之间的相似度，显然传统的哈希算法不能满足我们的需求。因此我们需要使用图像哈希。

不同图像哈希算法的比较

~~本节内容部分由ChatGPT生成。（真的不想写概念了~~ = =

dHash

dHash，也称为"差异哈希"，是一种用于图像处理和相似性比较的技术。它的主要思想是将图像转换为一种紧凑的表示形式，以便可以快速计算和比较图像之间的差异。 dHash 在图像搜索、相似图像检测、图片 deduplication（去重）、图像压缩等领域有着广泛的应用。

原理

dHash 基于图像的像素差异计算，将图像转换成一个二进制哈希码。具体原理如下：

预处理: 将输入图像转换为灰度图，以简化计算。
缩小尺寸: 缩小图像的尺寸，通常是 9x8 像素，这样可以得到一个小尺寸的图像。
求差: 计算每个像素的灰度差异，通常是右边像素减去左边像素的值。
哈希生成: 根据这些差异值，将图像转换为一个二进制哈希码。如果右边像素的值大于等于左边像素的值，则对应位设置为 1，否则为 0。

这样，每个图像都被表示为一个64位的哈希码，其中每一位代表了对应像素差异的比较结果。

pHash

pHash，全称为“感知哈希”（Perceptual Hash），是一种图像处理技术，用于计算图像的哈希值，以便比较和识别图像的相似性。与 dHash 不同，pHash 不仅仅关注像素差异，还考虑了人类视觉系统对图像的感知。pHash 在图像检索、内容识别、图像压缩等领域有广泛的应用。

原理

pHash 基于图像的颜色、纹理和结构特征，通过对这些特征进行提取和量化，生成一个紧凑的哈希码。具体原理如下：

预处理：将输入图像转换为灰度图或色彩空间（如YUV），以便更好地捕捉图像特征。
缩小尺寸：将图像缩小为一个较小的尺寸，通常是 8x8 或 16x16 像素，以减少计算量。
频域转换：对缩小后的图像进行离散余弦变换（DCT）等频域转换，以提取图像的频率特征。
量化：对频域转换后的系数进行量化，通常通过计算每个系数相对于均值的符号（正、负）来得到二进制位。
哈希生成：将量化后的系数映射到一个二进制序列，形成最终的 pHash 哈希码。

生成的 pHash 哈希码不仅考虑了图像的像素值，还捕捉了图像的结构、纹理等感知特征。

aHash

aHash，全称为“平均哈希”（Average Hash），是一种用于图像处理和相似性比较的简单而有效的技术。它通过计算图像的平均像素值来生成图像的哈希码，以便比较和识别图像的相似性。aHash 在图像检索、相似图像检测、图像压缩等领域有广泛的应用。

原理

aHash 的原理非常简单，它只考虑了图像的平均像素值，而没有涉及复杂的特征提取或变换。具体原理如下：

预处理：将输入图像转换为灰度图，以简化计算。
缩小尺寸：将图像缩小为一个小尺寸，通常是 8x8 像素，以减少计算量。
计算平均值：计算缩小后图像的所有像素的平均值。
生成哈希码：将图像的每个像素与平均值进行比较，如果像素值大于等于平均值，则对应位设置为 1，否则为 0。这样得到的二进制序列就是 aHash 哈希码。

生成的 aHash 哈希码简洁，但可以有效地捕捉图像的整体特征。

选择

不同哈希算法之间一般并没有一个最优选择，但是在我的测试下pHash算法在对图像细节差异的识别上要优于另外两种哈希。在实际应用中你可以对不同的图像哈希算法进行测试，选出你认为最优的即可。后面的比较过程都同时适用于上述三种图像哈希算法。

图像哈希的比较与VP树查询数据结构

通过图像哈希评估不同图像的差异

前文提到的三种哈希算法, 最后生成的都是一个64bit的哈希值, 一般使用一个unsigned int64_t存储. 在表示的时候也可以将其以二进制的形式按位表示, 例如 1101101100110101100010101110000101001110001001000010111110011000.

在比较不同图片的图片哈希时,只需要求这两个哈希的汉明距离即可, 在字符串表示中汉明距离即为两个相同长度的字符串对应位置的不同字符的数量. 而在二进制表示中, 则只需对两个哈希值求位异或然后统计结果中所有1的数量即可.得出的结果越小, 则两张图片越相近.

下面的算法可以用于快速统计一个ulong数据中所有1的数量.

private static readonly byte[] BIT_COUNTS =
{
    0,1,1,2,1,2,2,3, 1,2,2,3,2,3,3,4, 1,2,2,3,2,3,3,4, 2,3,3,4,3,4,4,5,
    1,2,2,3,2,3,3,4, 2,3,3,4,3,4,4,5, 2,3,3,4,3,4,4,5, 3,4,4,5,4,5,5,6,
    1,2,2,3,2,3,3,4, 2,3,3,4,3,4,4,5, 2,3,3,4,3,4,4,5, 3,4,4,5,4,5,5,6,
    2,3,3,4,3,4,4,5, 3,4,4,5,4,5,5,6, 3,4,4,5,4,5,5,6, 4,5,5,6,5,6,6,7,
    1,2,2,3,2,3,3,4, 2,3,3,4,3,4,4,5, 2,3,3,4,3,4,4,5, 3,4,4,5,4,5,5,6,
    2,3,3,4,3,4,4,5, 3,4,4,5,4,5,5,6, 3,4,4,5,4,5,5,6, 4,5,5,6,5,6,6,7,
    2,3,3,4,3,4,4,5, 3,4,4,5,4,5,5,6, 3,4,4,5,4,5,5,6, 4,5,5,6,5,6,6,7,
    3,4,4,5,4,5,5,6, 4,5,5,6,5,6,6,7, 4,5,5,6,5,6,6,7, 5,6,6,7,6,7,7,8,
};

public static int BitCount(ulong num)
{
    int count = 0;
    for (; num > 0; num >>= 8)
    {
        count += BIT_COUNTS[num & 0xff];
    }
    
    return count;
}

// Usage:
BitCount(hash1 ^ hash2);

如果想要计算相似度百分比, 则使用下面的表达式转换即可:64 - BitCount(hash1 ^ hash2) / 64.

使用VP树

接下来考虑存储一个图像集中所有图像哈希值的数据结构. 我们希望对这个数据结构进行建立以及区间查找(用于查找重复图片)的时间复杂度尽可能低. 考虑到汉明距离满足三角不等式定理,即任意哈希值 $h_1, h_2, h_3$ , 均满足:

$dist(h_1, h_2) + dist(h_2, h_3) \geq dist(h_1, h_3)$

因此可以使用VP Tree来存储图像哈希.

VP树简介

VP树是一个基于度量距离建立的树结构, VP树不关心给定数据的维度, 只需要给定可以计算得到满足三角不等式定理的距离计算函数, 即 $dist(p_x, p_y)$ 即可满足建立VP树的条件.

VP树是一个建立在度量空间(Metric Space)上的树，要想理解VP树必须先理解度量空间的概念：
想象一下，你失去了所有方向感，并被蒙住了双眼。你站在一个空旷的广场上，你只能通过声音感知周围的人与你的距离，但是你并不知道它们的方向。
在这样一个空间下，有下面几个基本法则：

如果你与一个人之间的距离=0, 那么你们就站在同一个地方。
距离是对称的，你到另一个人的距离与另一个人到你的距离永远相等。
假设你知道了与两个人（分别是A, B）的距离，你到B的距离永远小于或者等于你到A的距离加上A到B的距离，也就是说度量空间中任意三个点都满足三角不等式定理。

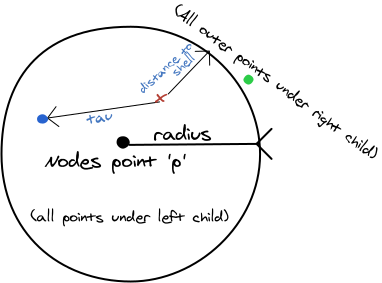
与二叉树等等其它树不同，VP树并不按数据与节点值本身的大小关系来划分左子树与右子树，因为度量距离永远为正。 VP树将子树节点数据与当前节点数据的距离通过一个半径(有时也叫权重)来划分，所有距离小于半径的数据都会进入左子树，而大于半径的数据都会进入右子树.

在二维空间中vp树的一个节点如下图所示。由于vp树在建立过程中只使用了度量距离，而度量距离存在于任意维度下，因此vp树可以非常轻松地扩展到任意维度。但是为了方便理解，接下来的图片中均在二维空间下举例。

vp-1

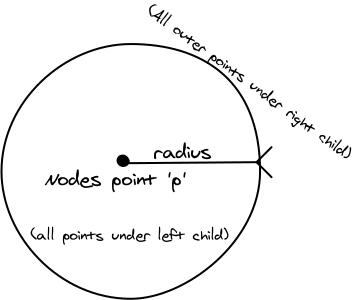
每个VP树节点数据结构需要存储节点本身的数据, 节点的半径 $r$ , 节点的左子树指针与右子树指针. 所有位于左子树的节点与该节点的距离都小于或等于 $r$ , 而位于右子树的节点与该节点的距离则都大于 $r$ .

VP树建立的平均时间复杂度为 $O(n\log n)$ , 而单次查询的时间复杂度为 $O(\log n)$

建立

首先选定第一个数据作为根节点 $p$ , 然后选定一个半径 $r$ (一般为所有其它点到根节点距离的中位数), 将所有距离小于 $r$ 的点放至左子树, 距离大于 $r$ 的点放至右子树, 然后递归建立子树.

区间搜索

假设我们需要搜索的数据值为 $p_0$ , 同时, 我们希望找到距离 $p_0$ 的距离小于 $d_0$ 的数据, 那么过程如下.

进入节点 $p$ , 首先计算 $d_p = dist(p_0, p)$ , 如果 $d_p \leq d_0$ , 则将 $p$ 加入结果序列中.

接下来分下面两步进行:

如果 $d_p - d_0 \leq r$ , 则代表左子树(即下图中 $c_i$ 圆内)中可能包含需要搜索的点(期待搜索范围为下图中 $c_0$ 圆内), 因此需要对 $p$ 的左子树进行递归搜索. 如下图所示.
$d_p - d_0 \leq r$ 搜索左树 $d_p - d_0 \gt r$ 不搜索左树
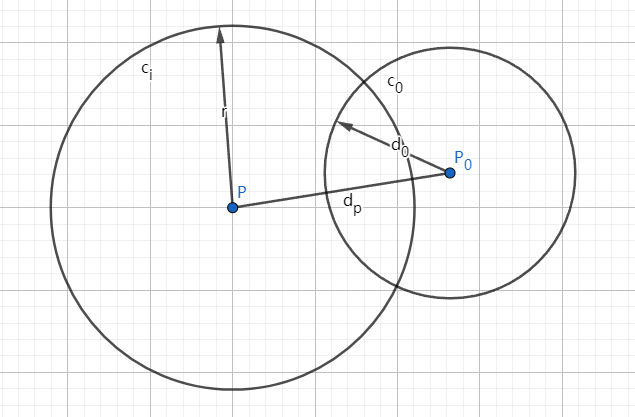
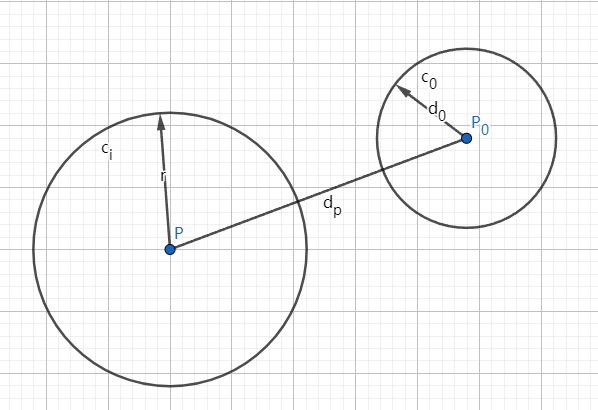
如果 $d_p + d_0 \geq r$ , 则代表右子树(即下图中 $c_i$ 圆外)中可能包含需要搜索的点(期待搜索范围为下图中 $c_0$ 圆内), 因此需要对 $p$ 的右子树进行递归搜索. 如下图所示.
$d_p + d_0 \geq r$ 搜索右树 $d_p + d_0 \lt r$ 不搜索右树

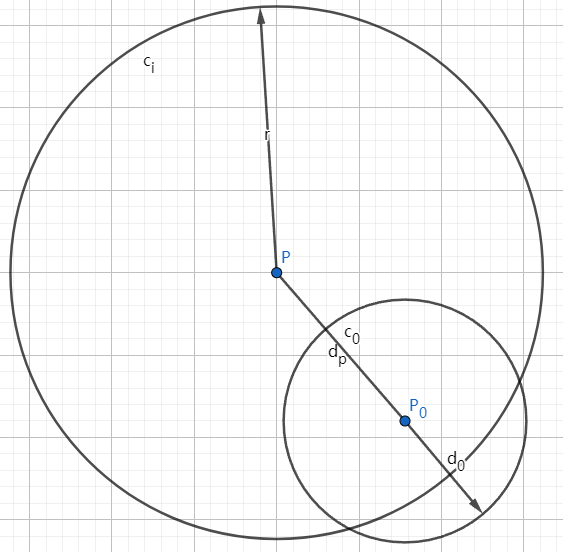
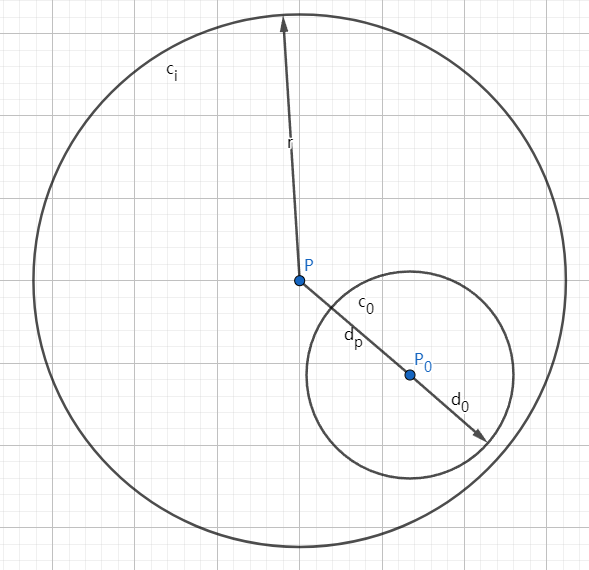
与二叉树不同, $d_p - d_0 \leq r$ 与 $d_p + d_0 \geq r$ 可能同时成立! 因此在某些情况下你必须同时递归搜索左子树与右子树.

vp-2

上文中对vp树概念的介绍部分参考了这篇文章：http://stevehanov.ca/blog/?id=130
如果想要了解VP树的细节, 建议看看上面的文章。
~~人家讲的比我好太多了~~

使用并查集集合距离较近的图片

建立完成VP树后, 给定任意图片哈希就可以查询出与该图片距离在给定值以下的图片了. 但是我们希望得到的是一个相似图片组的列表, 即img[][], 因此接下来还需要用并查集进行集合操作.

并查集算法因为非常简单且著名, 我这里就不过多介绍了, 如果想要了解可以看看oi-wiki中的文章. 在使用路径压缩后, 并查集的所有操作的时间复杂度都非常接近于 $O(1)$ .

Anyway, 我们这里要做的就是遍历待查询列表中的所有图片, 通过前面建立的VP树找到与它相似度在给定范围内的所有图片 (注意: 如果待查询数据集与前面用于建树的数据集是同一个的话,那么这里的结果里必然有一张是它本身, 不过在并查集中将自己与自己合并这个操作是合法的.)

建树与集合代码如下:

// Building Data Hashes
_imgTree = new VpTree<ImgFile>(ImgFiles.ToArray(), (x, y) => (int)x.ImageDiff(y));

Dsu dsu = new(ImgFiles.Count);
foreach (var item in ImgFiles)
{
    var result = _imgTree.SearchByMaxDist(item, Similarity);
    result.ForEach(t => dsu.Union(item.Id, t.Item1.Id));
}

将最终结果整理为列表

使用哈希表,用并查集根节点的id作为索引即可. 代码如下:

Dictionary<int, List<ImgFile>> groupsDict = new();
foreach (var item in ImgFiles)
{
    var g = dsu.Find(item.Id);
    // If the root is the item itself, don't add it to the dict for now.
    // This can reduce the number of List<> needs to be created.
    if (g == item.Id) continue;
    if (groupsDict.TryGetValue(g, out var value))
    {
        value.Add(item);
    }
    else
    {
        groupsDict.Add(g, new List<ImgFile> { item });
    }
}

List<List<ImgFile>> resultGroups = new();
foreach (var (id, value) in groupsDict)
{
    // Add the root element to the list since we've ignored it just now.
    value.Add(ImgFiles[id]);
    resultGroups.Add(value);
}

注意在这个过程中我们舍弃了所有只有一个元素的列表. 得到的resultGroups就是所有相似的两张或以上的图像组了.

时间复杂度的计算

计算 $n$ 张图片哈希 $O(n)$ 当然由于此步涉及图片的读取转换等，需要的计算量较大，建议通过多线程优化来提升速度。
建立VP树 $O(n\log n)$
查询 $n$ 次VP树 $O(n\log n)$
整理结果 $O(n)$

因此总体时间复杂度为 $O(n\log n)$ , 在可接受范围内了。

项目实现

上文中所写的哈希计算与对比，都实现在了我写的PixNinja.GUI项目中：
https://github.com/hv0905/PixNinja.GUI
截至发文时，这个项目的主要功能都基本可以使用（虽然UI丑了点）

局限

图像哈希虽然对经过调色、压缩、变更分辨率等等操作的图像具有较好的鲁棒性，但是对于经过旋转、翻转、裁剪等操作的鲁棒性较低，因此图像哈希只能完成非常简单的图像搜索功能。如果你对图像搜索功能的要求更加高，例如希望构建一个类似于google image search或ascii2d的图像搜索引擎，那么图像哈希就不够用了。这种图像搜索引擎一般使用了如图片特征点提取等等更高级的算法，同时也需要为经过特征点提取后的索引数据设计合理的数据结构进行快速检索，这些算法就不在本文的讨论范围内了~~（主要是我也不会）~~
图像哈希由于在生成时涉及到将图片压缩至8 x 8 或是 9 x 8 的操作，因此不可避免地会丢失部分图像细节。这导致通过图片哈希比较将无法分辨图像中细微的不同，这个问题在面对一些galgame差分cg时尤为明显，如下面是两张表情不一样的galgame差分cg以及它们压缩到8x8之后的样子：
原图压缩处理后
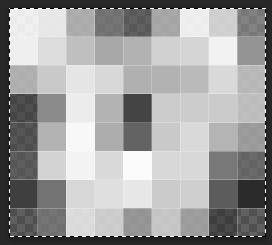
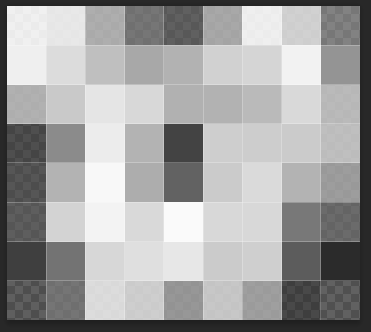
两张处理后的图片几乎看不出任何细节，这也让这两张图片的图片哈希极为相似或完全一致。要想解决这类问题的一个办法就是加大哈希的长度，例如将图片压缩至16 x 16并取256位哈希长度，但是这样又会大幅增加哈希计算与比对时的计算量。
不过在处理大多数图片的时候无需过多担心这样的问题，因为其它图片通常不会具有很高的相似度。